Nontransitive Game with Coin Combinations

On 11 September 2009 Derren Brown introduced many for the first time to a non-transitive game where a person who goes second, flipping coins in the same number as a partner going first, will, according to probability, predict the coin patterns more correctly and thus sooner than the first partner.

A player chooses a combination of three coin throws. The combination chosen determines which combination of three the second player chooses. The two players each throw their coins, three by the first player and three by the second. They do this for any number of throw combinations to achieve the set number (three or more - say ten - successful combinations). In probability the second player gets the successful combinations first.

He called it "finding predictability in randomness" and is found in "deep maths". The Channel 4 website does not explain how it works. Mick's Mathematical Puzzles Solution 13Click for a mathematical explanation does explain, mathematically.

Here is a more wordy explanation...

Putting unevenness into evenness while maintaining the unevenness in the packaging means... unevenness. Such is essential for an uneven and therefore predictable (by probability) outcome.

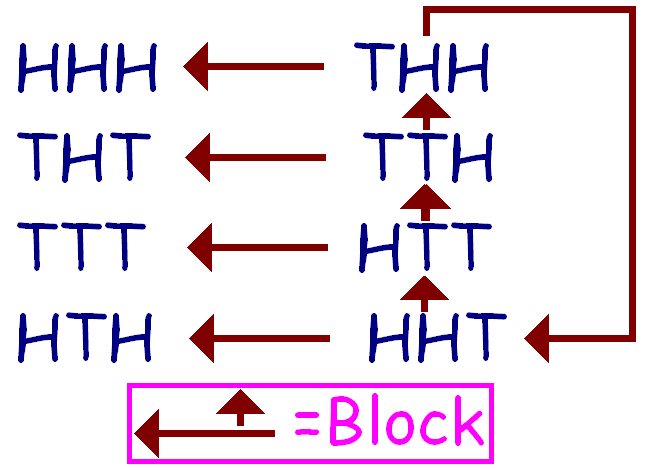
The key is that one set of coin combinations in effect blocks another set of coin combinations. In fact, each of four combinations block two other combinations each while four combinations block none.

The method of countering any first combination by copying the middle one, reversing it and moving it to the front and then dropping off the fourth right to make three again is crucial. It's like a twist in a ribbon.

The fact is that such a method cannot produce HHH, THT, TTT or HTH, which are evenly spaced unevenly packaged. These combinations block nothing. The method always produces THH, TTH, HTT and HHT, which are unevenly spaced in the uneven package. Each of these blocks twice.

Why is blocking important? Think of rock, scissors and paper, another nontransitive game but one where there is no packaging to preserve superiority: there are no cul-de-sacs in that game.

HHH and TTT are one in eight combinations and thus very weak - it only takes a T and a H to block each respectively. Thus there is a 7 to 1 chance of these being beaten. No doubt Derren Brown impressed or knew his first player would pick HHH. THT and HTH being quite even have a 2 to 1 chance against them (still decisive) where two coins together change (from TTH and HHT respectively - thus affecting only an unevenness). TTH over THH and HHT over HTT change one letter and also close - again 2 to 1 each. THH over HHT and HTT over TTH changes two outer ones (they are affecting the evenness inside the unevenness!) and these are 3 to 1.

THH and HTT are thus the strongest combinations, with advantages 7 to 1 and 3 to 1: but you cannot pick these first! If you do, the nontransitive game allows 2 to 1 against each. So the person who goes first always loses.

Yes it is still quite difficult to understand but the error is to let the evenness of the coin tossing cover over the unevenness of the packaging making possible the uneven rule that amounts to 'blocking'. It is the blocking that stops something happening allowing the other to come through.