Because there was a need to calculate large numbers a device was necessary using a zero number system. When all marks, counters or balls are at one end (two ends!) the result is a zero in that position. The first abacus might have been a sand covered table but certainly became a ruled table with counters, common in Europe until the 1500s and less common beyond. Balls on rods in a framework are much more portable. Values of the beads from units upward were varied but were regular in increasing magnitude within each abacus. Only in recent years have electronic calculators superseded the abacus in Russia, China, Japan and in some Arab states.
In an abacus today, each rod to the left is to the power of ten, as in our decimal mathematics system, because there are ten beads on each rod. If there were 16 beads then this would be hexadecimal to the power of 16 on each rod left. This simple decimal abacus operates like this, using the example of starting with 458 and intending to add 247:

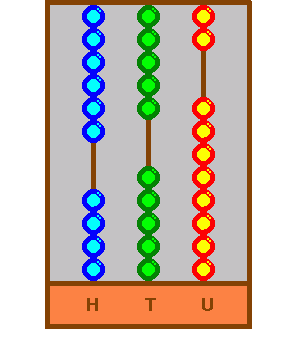
First of all the 458 has four beads at the bottom of the 100 rod, five beads at the bottom of the tens rod and eight at the bottom of the units rod. Of the 247 to add, the calculation starts with the units at the right. Seven is added to the eight at the bottom, but because there were only two left at the top, only two can go downwards:
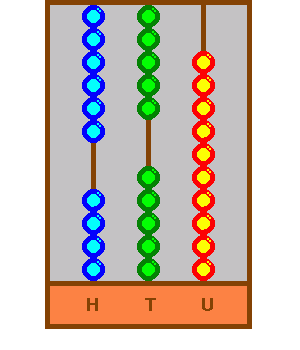
There are five still to add. The solution is that five, instead of coming down, must go up (including the two that came down).
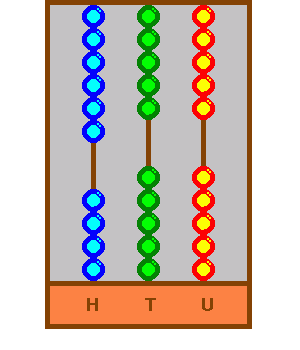
However, because five go up, there is a price to pay. One bead must come down in the tens rod before the calculation continues. This completes the units calculation, as below:
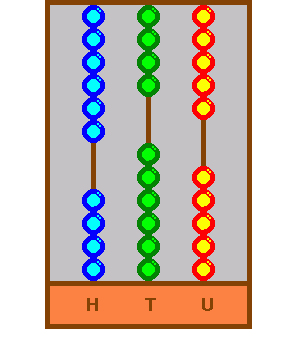
Having added seven of the 247, now is the time to add 40. This means four beads of the tens rod (that is 40) must come down. However, something odd happens. All the beads are down and although it might be thought that this completes the movement, it does not...
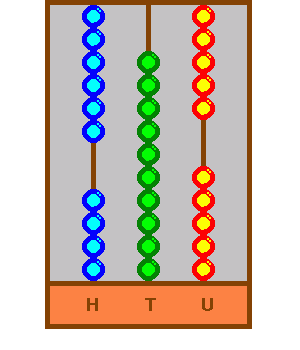
This is crucial. The above cannot be allowed. All the beads cannot stay down, because this is the next power up (10 X 10 is 100) and it shows that the all important Indian to Arab to the West and subsequently to the world zero is those ten beads when together. This is the design fault in the abacus, or rather in our interpretive needs, discussed at the end. We need zero, and so all ten beads must go up, leaving a gap - nothing at all - or the zero, as shown:
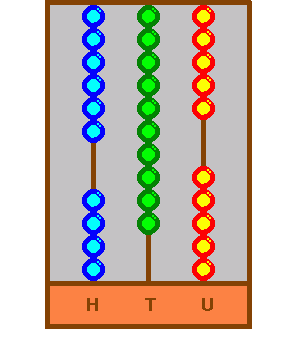
The price to pay, before the calculation can move on, is a bead then must drop in the hundred column. So this happens:
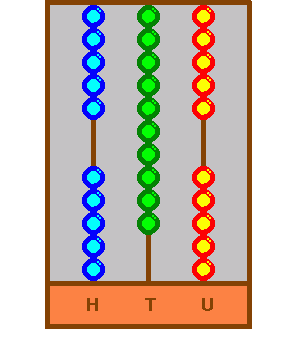
Finally, with the forty seven added, the remaining two hundred can be added by dropping down two beads on the hundred power rod:
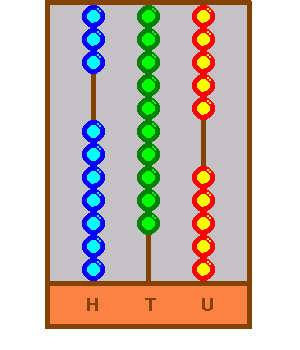
The result is seven beads down on the first rod, or seven hundred, no beads down on the second rod, and therefore zero tens, and five beads down on the last rod, representing five. This is 705 and the calculation is successful.
The abacus therefore shows a need for rules of movement:
The abacus therefore changes arithmetic into counting and movement:
The movement is shown:

Subtraction has its own reversals and no reversals, but there is further explanation before coming to this.
The puzzle with the abacus is that it seems to start with 1 and so puts the operation of zero to the end. In fact this end zero is caused by an operation going into the next power up. Ten beads are needed to do this, but there are only nine substantive numbers, and one bead is a mathematical property but no substantive thingy number. Thus when ten beads are down, the zero comes into play. Now a rod may stay visually empty from the beginning representing zero. But if this was done consistently, there would be one bead representing the zero down at the bottom: it is not, because we intuitively give all beads substance as well as mathematical property. Therefore we, as thingy-counting people, leave the beads at the top. So this is why the reverse rule is needed, so that it accords with our vision and thingy-like interpretation.
Computers do this properly with the hexadecimal system as presented (fundamentally it is binary, but humans need to see bigger powers), because they start with the zero, 0, and go to 9 (with the numbers symbolism) and continue with A to F borrowing the alphabet for those remaining symbols. The last one is 15 (in decimal) to make the 16th. 16 in hexadecimal is 10, of course. So one of those numbers is without substance but with a property of zero, and it is the first one. This is what the Romans could not understand, or at least could not symbolise and therefore use, except through substantive numbers that incorporated zero by omission. The number 705 they often symbolised with CCCCCCCV. There are jumps there where there are no physical symbolised blocks of numbering. Properly speaking, we do count from 0 to 9 and then it is 10 onward. With the abacus, the tenth bead employs a reverse rule to put things right after the physical misinterpretation. We humans get it right, however, when we look at buildings. The first floor is the second storey, the correct counting method being the floors approach, but the intuitive thingy substance-like interpretation is the storeys, just as with an abacus. The abacus beads should really be 0 to 9, all ten of them.
This is about adding. With substraction the same counting procedures apply but in the opposite direction for each rod (but they go along the rods in the same way). The counting will reverse direction in the beads, but if ten beads go to the top they can stay there: nothing needs to come down. That is because the zero bead went first and has done its job. They do not need to come down again. If there is a reverse in the direction, then one bead on the next rod along has to go up before that rod's calculation is carried out.
The Hindus called their discovery of the zero a sunyabindi or just sunya, meaning empty or void. The Arabic took this as safr or assafr. Then came zephirum and so zero in Calandi's Arithmetic in 1491 (Churchill, 1961, 37-39). The following Hindu symbol of Aum or Om, the sound of the eternal, shows the zero (to the right, highlighted in red), being alongside the trimurti (Brahma, Vishnu and Shiva).
Churchill, E. M. (1961), Counting and Measuring: An Approach to Number Education in the Infant School, London: Routledge and Kegan Paul.
Adrian Worsfold
All images originate with Adrian Worsfold©: however, copying and further use is welcomed for educational purposes (I would appreciate an email if this happens).